Contents
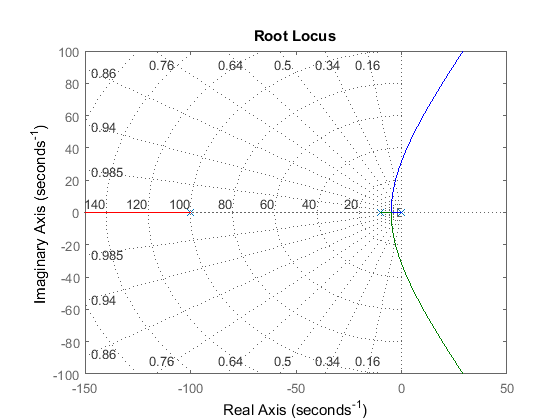
P6.1 DC motor
clear variables
G=zpk([],[0 -10 -100],5000);
disp('Root locus plot:')
rlocus(G),grid
axis([-150 50 -100 100])
k=0.95
Kstab=21.9
Root locus plot:
k =
0.9500
Kstab =
21.9000
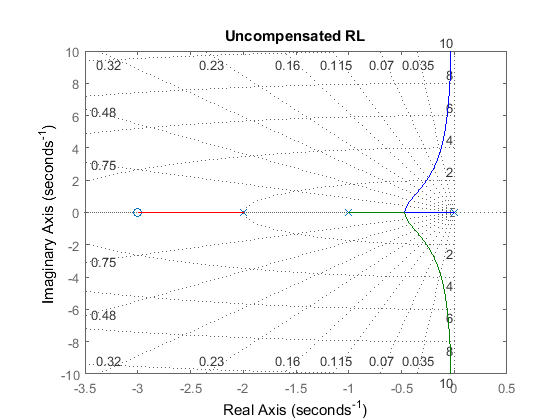
P6.2 Dynamic system
G=zpk([-3],[0 -1 -2],1);
disp('Root locus plot:')
figure(1), rlocus(G), grid
title('Uncompensated RL')
disp('Range of K for stability:')
Kstab=margin(G)
s1=-2+j*2;
h=freqresp(G,s1);
disp('Compensator angle:')
th=180-angle(h)*180/pi
disp('Phase-lead compensator')
Klead=zpk(-1,-8,1)
h=evalfr(Klead*G,s1);
disp('Compensated angle:')
th=angle(h)*180/pi
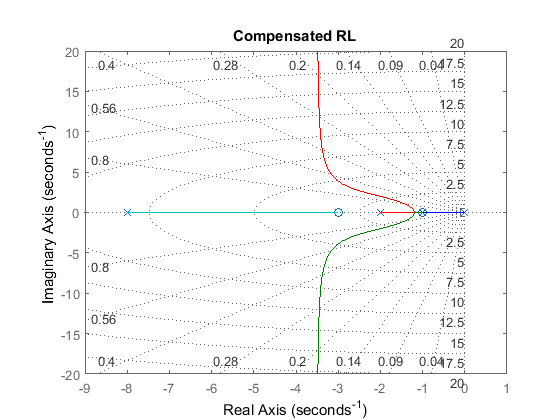
figure(2), rlocus(Klead*G), grid
title('Compensated RL')
Root locus plot:
Range of K for stability:
Kstab =
Inf
Compensator angle:
th =
98.1301
Phase-lead compensator
Klead =
(s+1)
-----
(s+8)
Continuous-time zero/pole/gain model.
Compensated angle:
th =
180
P6.3 Dynamic system
disp('Velocity error constant:')
D=zpk(0,[],1);
kv=dcgain(Klead*D*G)
kv1=10/kv;
disp('Lead-lag compensator')
Klag=zpk(-.1,-.1/kv1,1);
K=Klead*Klag
rlocus(K*G), grid
T=feedback(17.5*K*G,1);
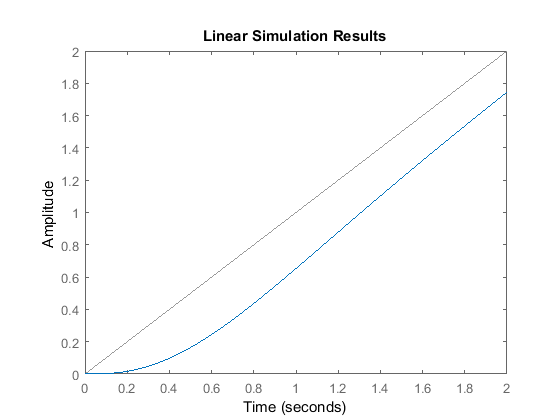
disp('Ramp response:')
t=0:.01:2;
lsim(T,t,t)
disp('Controller realization:')
syms ri ci rf cf
comp1=solve(ri*ci-1, rf*cf-1/8, rf/ri-2, ci,cf,rf);
disp('Stage 1:')
disp('Ci='),disp(comp1.ci)
disp('Cf='),disp(comp1.cf)
disp('Rf='),disp(comp1.rf)
comp2=solve(ri*ci-10, rf*cf-160, rf/ri-1, ci,cf,rf);
disp('Stage 2:')
disp('Ci='),disp(comp2.ci)
disp('Cf='),disp(comp2.cf)
disp('Rf='),disp(comp2.rf)
Velocity error constant:
kv =
0.1875
Lead-lag compensator
K =
(s+1) (s+0.1)
------------------
(s+8) (s+0.001875)
Continuous-time zero/pole/gain model.
Ramp response:
Controller realization:
Stage 1:
Ci=
1/ri
Cf=
1/(16*ri)
Rf=
2*ri
Stage 2:
Ci=
10/ri
Cf=
160/ri
Rf=
ri
P6.4 Flexible beam
G=tf(100,[1 1 100]);
K0=pid(1,1,1,.001);
Kpid=pidtune(G,K0);
disp('PID controller')
zpk(Kpid)
disp('Controller realization:')
syms ri ci rf cf
disp('PI stage:')
comp=solve(ri*ci-1/12.56, ri*cf-1/12.56, ri,cf);
disp('Ri='),disp(vpa(comp.ri,3))
disp('Cf='),disp(comp.cf)
disp('PD/Phase-lead stage:')
comp=solve(ri*ci-1/5.2, rf*cf-1/5233, rf/ri-2.1744, ri,rf,cf);
disp('Ri='),disp(vpa(comp.ri,3))
disp('Rf='),disp(vpa(comp.rf,3))
disp('Cf='),disp(vpa(comp.cf,3))
PID controller
ans =
2186.9 (s+12.56) (s+5.203)
--------------------------
s (s+5233)
Continuous-time zero/pole/gain model.
Controller realization:
PI stage:
Ri=
0.0796/ci
Cf=
ci
PD/Phase-lead stage:
Ri=
0.192/ci
Rf=
0.418/ci
Cf=
4.57e-4*ci
P6.5 DC motor
G=zpk([],[0 -10 -100],5000);
D=zpk(0,[],1);
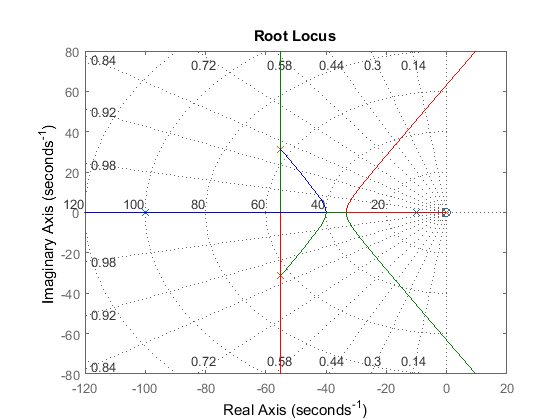
disp('Root locus:')
rlocus(D*G), grid, hold
disp('Minor loop gain:')
kf=0.6
disp('Minor loop transfer function:')
Gm=feedback(G,kf*D)
rlocus(Gm), hold
disp('Cascade controller gain:')
k=5
Root locus:
Current plot held
Minor loop gain:
kf =
0.6000
Minor loop transfer function:
Gm =
5000
---------------------
s (s^2 + 110s + 4000)
Continuous-time zero/pole/gain model.
Current plot released
Cascade controller gain:
k =
5
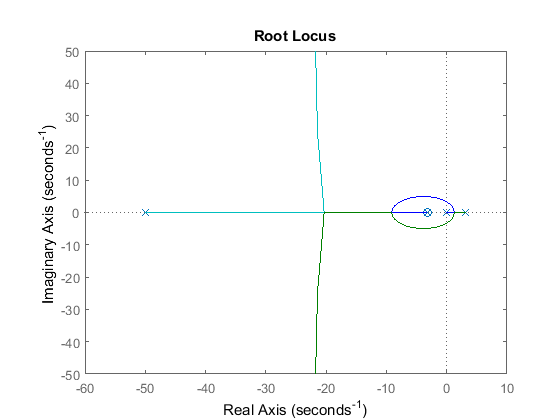
P6.6 Human postural dynamics
G=tf([10],[1 0 -10]);
disp('Phase-lead design:')
Klead=zpk(-sqrt(10),-50,1)
disp('Phase-lag design:')
Klag=tf([1 sqrt(10)],[1 .1])
figure(1), rlocus(Klead*Klag*G)
disp('Compensator:')
K=100*Klead*Klag
disp('Position error constant:')
dcgain(K*G)
disp('Closed-loop damping:')
T=feedback(K*G,1)
damp(T)
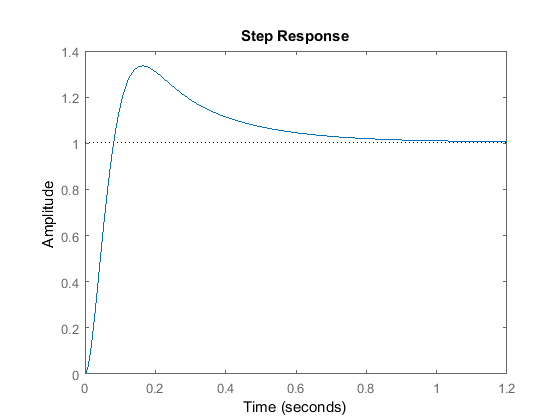
disp('Step response:')
figure(2), step(T)
Phase-lead design:
Klead =
(s+3.162)
---------
(s+50)
Continuous-time zero/pole/gain model.
Phase-lag design:
Klag =
s + 3.162
---------
s + 0.1
Continuous-time transfer function.
Compensator:
K =
100 (s+3.162)^2
---------------
(s+50) (s+0.1)
Continuous-time zero/pole/gain model.
Position error constant:
ans =
-200.0000
Closed-loop damping:
T =
1000 (s+3.162)^2
----------------------------------------
(s+4.917) (s+3.162) (s^2 + 42.02s + 640)
Continuous-time zero/pole/gain model.
Pole Damping Frequency Time Constant
(rad/seconds) (seconds)
-3.16e+00 1.00e+00 3.16e+00 3.16e-01
-4.92e+00 1.00e+00 4.92e+00 2.03e-01
-2.10e+01 + 1.41e+01i 8.31e-01 2.53e+01 4.76e-02
-2.10e+01 - 1.41e+01i 8.31e-01 2.53e+01 4.76e-02
Step response: