Contents
P8.1 PID controller emulation
clear variables
Ts=0.1;
kp=20; kd=10; ki=1;
I=tf(1,[1 0]);
Id=c2d(I,Ts,'impulse');
Kz=kp+kd/Id+ki*Id;
disp('PID controller emulation:')
tf(Kz)
disp('Controller input/output:')
Ad=[0 1; 0 0]; Bd=[Ts; 1];
Cd=[ki -kd/Ts]; Dd=kp+ki*Ts+kd/Ts;
f1=@(x,u) [Ad*x+Bd*u; Cd*x+Dd*u];
e=rand(1,10); x=rand(2,1); u=Cd*x+Dd*e;
for i=1:length(e), xy=f1(x,e(i)); u(i+1)=xy(3); x=xy(1:2); end
e,u
PID controller emulation:
ans =
12.01 z^2 - 22 z + 10
---------------------
0.1 z^2 - 0.1 z
Sample time: 0.1 seconds
Discrete-time transfer function.
Controller input/output:
e =
Columns 1 through 7
0.7350 0.9706 0.8669 0.0862 0.3664 0.3692 0.6850
Columns 8 through 10
0.5979 0.7894 0.3677
u =
Columns 1 through 7
79.8078 79.8078 43.2333 7.8905 -75.2790 36.2611 7.8200
Columns 8 through 11
45.7554 3.7476 35.7533 -34.1044
P8.2 Controller emulation
G=tf(1,[1 0 0]);
Ts=.05;
Gz=c2d(G,Ts);
Gc=zpk([-.1 -1],[-.01 -6], 20);
disp('Controller emulation:')
disp('PZ matching')
Kz=c2d(Gc,Ts,'matched')
Tz1=feedback(Kz*Gz,1);
disp('Bilinear transform')
Kz=c2d(Gc,Ts,'tustin')
Tz2=feedback(Kz*Gz,1);
disp('ZOH')
Kz=c2d(Gc,Ts)
Tz3=feedback(Kz*Gz,1);
disp('Step response:')
T=feedback(Gc*G,1);
step(Tz1,Tz2,Tz3,T)
legend('PZ matching','Bilinear','ZOH', 'Continuous-time')
Controller emulation:
PZ matching
Kz =
17.754 (z-0.995) (z-0.9512)
---------------------------
(z-1) (z-0.7408)
Sample time: 0.05 seconds
Discrete-time zero/pole/gain model.
Bilinear transform
Kz =
17.866 (z-0.995) (z-0.9512)
---------------------------
(z-1) (z-0.7391)
Sample time: 0.05 seconds
Discrete-time zero/pole/gain model.
ZOH
Kz =
20 (z-0.9949) (z-0.9574)
------------------------
(z-1) (z-0.7408)
Sample time: 0.05 seconds
Discrete-time zero/pole/gain model.
Step response:
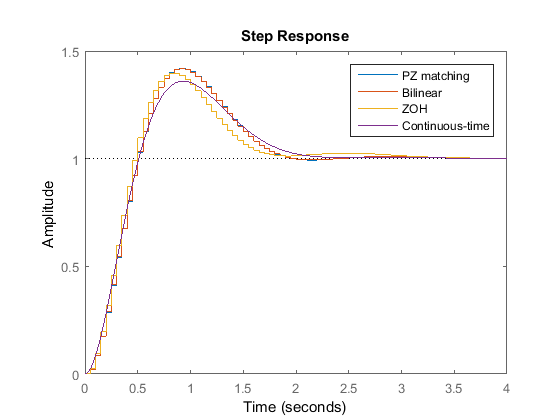
P8.3 Flexible beam
G=tf(100,[1 1 100]);
disp('PID controller:')
K0=pid(1,1,1,.001);
Kpid=pidtune(G,K0);
Ts=.001;
Gz=c2d(G,Ts);
Kz=c2d(Kpid,Ts)
T=feedback(Kpid*G,1);
Tz=feedback(Kz*Gz,1);
disp('Step response:')
step(Tz,T)
PID controller:
Kz =
Ts 1
Kp + Ki * ------ + Kd * -----------
z-1 Tf+Ts/(z-1)
with Kp = 7.42, Ki = 27.3, Kd = 2.19, Tf = 0.00101, Ts = 0.001
Sample time: 0.001 seconds
Discrete-time PIDF controller in parallel form.
Step response:
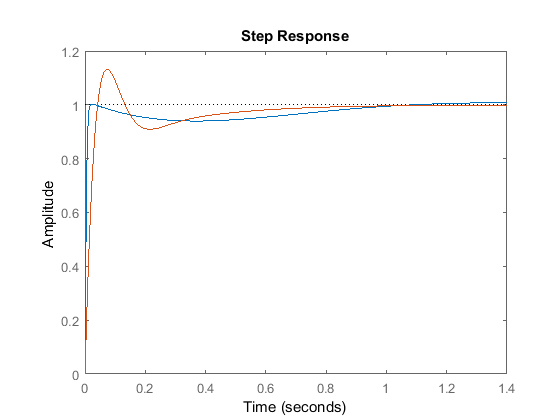
P8.4 Automobile
disp('Automobile model:')
G=tf([28 120],[1 7 14]);
Ts=.01;
disp('Discrete-time model:')
Gz=c2d(G,Ts)
figure(1), rlocus(Gz), grid
k=2;
Tz=feedback(k*Gz,1);
T=feedback(k*G,1);
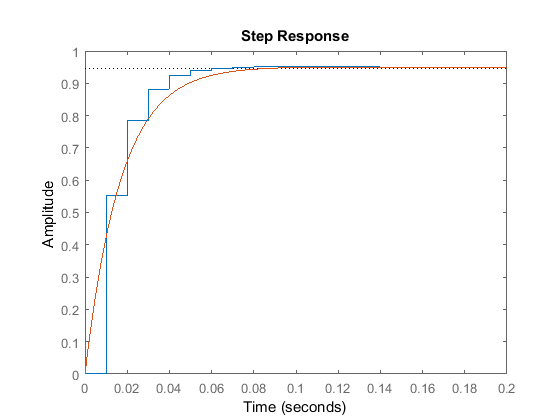
disp('Step response:')
figure(2), step(Tz,T)
Automobile model:
Discrete-time model:
Gz =
0.2762 z - 0.2646
----------------------
z^2 - 1.931 z + 0.9324
Sample time: 0.01 seconds
Discrete-time transfer function.
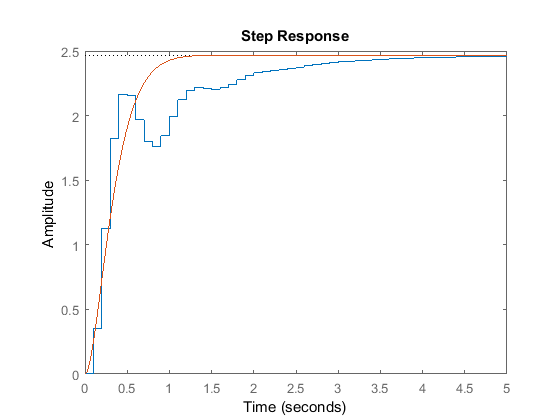
Step response:
P8.5 Dynamic system
G=zpk([-3],[0 -1 -2],1);
Ts=.5;
Gz=c2d(G,Ts);
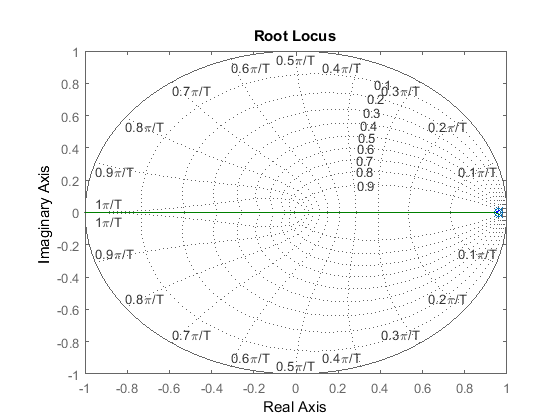
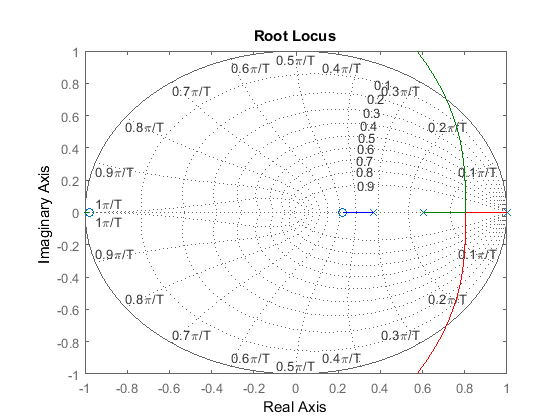
figure(1), rlocus(Gz), grid
axis([-1 1 -1 1])
k=.2;
disp('Discrete-time model:')
Tz=feedback(k*Gz,1)
T=feedback(k*G,1);
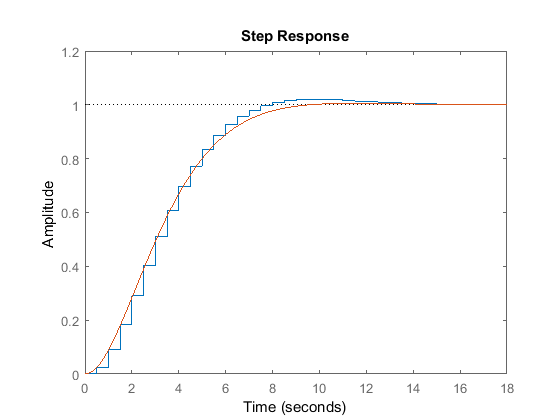
disp('Step response:')
figure(2), step(Tz,T)
Discrete-time model:
Tz =
0.024218 (z-0.2218) (z+0.9794)
----------------------------------
(z-0.3449) (z^2 - 1.605z + 0.6623)
Sample time: 0.5 seconds
Discrete-time zero/pole/gain model.
Step response:
P8.6 Human postural dynamics
G=tf([10],[1 0 -10]);
Klead=zpk(-sqrt(10),-10-sqrt(10),7);
Ts=.1;
disp('Discrete-time models:')
disp('Plant:')
Gz=c2d(G,Ts);
disp('Controller:')
Kz=c2d(Klead,Ts);
disp('Step response:')
Tz=feedback(Kz*Gz,1);
T=feedback(Klead*G,1);
step(Tz,T)
Discrete-time models:
Plant:
Controller:
Step response: