Contents

% Skills Assessment - Chap 5

P5.1 DC Motor

clear variables
syms V ia th om R L J b kt kb k real
syms s
%Motor equations in Laplace variable
eq1=R*ia+kb*om-V;
eq2=(J*s+b)*om-kt*ia;
eq2=subs(eq2,ia,solve(eq1,ia));
eq3=s*th-om;
%State equations
[A1,B1]=equationsToMatrix([eq2,eq3],[om,th]);
A2=subs(A1,[R,J,b,kt,kb,s],[1,.01,.05,.1,.1,0]);
B2=subs(B1,[R,kt,V],[1,.05,1]);
A=-double(A2);
B=double(B2);
G=ss(A,B,[1 0],0);
disp('Characteristic polynomials:')
[num,den]=tfdata(G,'v');
p=k*num+den;
vpa(p,2)
%
K=tf([1 10],1);
[num,den]=tfdata(K*G,'v');
p=k*num+den;
vpa(p,2)
%
K=tf([5 1],[1 0]);
[num,den]=tfdata(K*G,'v');
p=k*num+den;
vpa(p,2)
%
K=tf([1 5 1],[1 0]);
[num,den]=tfdata(K*G,'v');
p=k*num+den;
vpa(p,2)
%
K=tf([1 10],[1 1]);
[num,den]=tfdata(K*G,'v');
p=k*num+den;
vpa(p,2)
%
K=tf([1 1],[1 10]);
[num,den]=tfdata(K*G,'v');
p=k*num+den;
vpa(p,2)

Characteristic polynomials:
ans =
[ 1.0, 0.05*k + 0.06]
ans =
[ 0.05*k + 1.0, 0.5*k + 0.06]
ans =
[ 1.0, 0.25*k + 0.06, 0.05*k]
ans =
[ 0.05*k + 1.0, 0.25*k + 0.06, 0.05*k]
ans =
[ 1.0, 0.05*k + 1.1, 0.5*k + 0.06]
ans =
[ 1.0, 0.05*k + 10.0, 0.05*k + 0.6]

P 5.2 PID controller

disp('PID controller:')
K0=pid(1,1,1,.01);
K=pidtune(G,K0)
T=feedback(K*G,1);
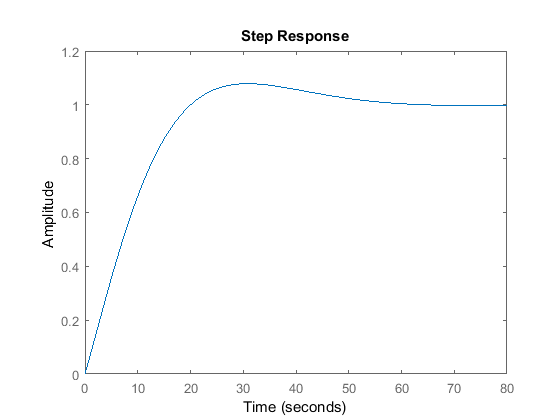
disp('Step response:')
step(T)

PID controller:

K =
 
             1            s    
  Kp + Ki * --- + Kd * --------
             s          Tf*s+1 

  with Kp = 1.61, Ki = 0.192, Kd = -0.972, Tf = 4.41
 
Continuous-time PIDF controller in parallel form.

Step response:

Published with MATLAB® R2015b